티스토리 뷰
오차 역전파법 : 신경망의 가중치 매개변수에 대한 손실함수의 기울기를 빠르게 구하기 위함 (효율적으로)
계산 그래프 : 계산 과정을 그래프로 나타낸 것 (노드와 엣지 이용)

순전파 : 순서대로 진행한 것

역전파 : 역으로 계산한 것 => 이를 이용해 미분을 구한다.
연쇄 법칙 이용해 계산 그래프의 역전파 계산


덧셈의 경우 z=x+y 일 때 dz/dx=1, dz/dy=1 이므로 역전파시 E값에 1을 곱한다. (E=dL/dz)

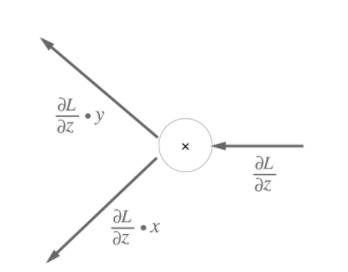
곱셈의 경우 z=x*y 일 때 dz/dx=y, dz/dy=x 이므로 역전파시 x방향 E값에 y, y방향 E값에 x를 곱한다. (E=dL/dz)
예제) 다음 그림과 같은 경우에서 역전파법으로 계산 그래프를 완성하자.

코드
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y
dy = dout * self.x
return dx, dy
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1
# 가격 계산
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
mul_apple_price = mul_apple_layer.forward(apple, apple_num)
mul_orange_price = mul_orange_layer.forward(orange, orange_num)
add_apple_orange_price = add_apple_orange_layer.forward(mul_apple_price, mul_orange_price)
total_price = mul_tax_layer.forward(add_apple_orange_price, tax)
print("total_price={}".format(total_price))
# 미분 계산
dprice = 1
dapple_orange, dtax = mul_tax_layer.backward(dprice)
print("dprice={}, dapple_orange={}, dtax={}".format(dprice, dapple_orange, dtax))
dapple_mul, dorange_mul = add_apple_orange_layer.backward(dapple_orange)
print("dapple={}, dorange={}".format(dapple_mul, dorange_mul))
dapple, dapple_num = mul_apple_layer.backward(dapple_mul)
dorange, dorange_num = mul_orange_layer.backward(dorange_mul)
print("dapple={}, dapple_num={}, dorange={}, dorange_num={}".format(dapple, dapple_num, dorange, dorange_num))

total_price=715.0000000000001
dprice=1, dapple_orange=1.1, dtax=650
dapple=1.1, dorange=1.1
dapple=2.2, dapple_num=110.00000000000001, dorange=3.3000000000000003, dorange_num=165.0'딥러닝' 카테고리의 다른 글
| 오차역전파법 구현 (0) | 2021.01.14 |
|---|---|
| 오차역전파법 - Affine, Softmax 구현 (0) | 2021.01.14 |
| 오차역전파법 - 활성화 함수 계층 구현하기 (0) | 2021.01.14 |
| 신경망 학습 알고리즘 구현 (0) | 2021.01.12 |
| 신경망 학습 절차 (0) | 2021.01.11 |
댓글
