티스토리 뷰
1916번: 최소비용 구하기
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
출발 지점에서 도착 지점까지의 최소 거리를 구하는 문제입니다. 음의 가중치가 입력으로 들어오지 않으므로 다익스트라 알고리즘이 적합합니다. 시간 제한이 0.5초라 MinHeap(우선순위 큐)를 이용하였습니다.
복잡도
기본 다익스트라 : O( E+V^2 ) = O( V^2 )
우선순위 큐 이용 : O( (E+V) log(V) )
기본적인 다익스트라 구조에서는 최단 거리를 가진 노드를 찾기 위해 선형 탐색을 하여 찾는다. 하지만 우선순위 큐를 이용해 거리를 내림차순으로 정렬하면 최단 거리를 가진 노드를 바로 찾을 수 있다. (우선순위 큐는 기본적으로 오름차순 정렬이므로 내림차순이 되도록 만들어준다.)
우선순위 큐를 활용한 다익스트라 알고리즘은 다음과 같습니다.
그래프 노드와 가중치가 아래와 같다고 합시다. (편의를 위해 양방향으로 하였고, A를 시작노드로 잡겠습니다.)
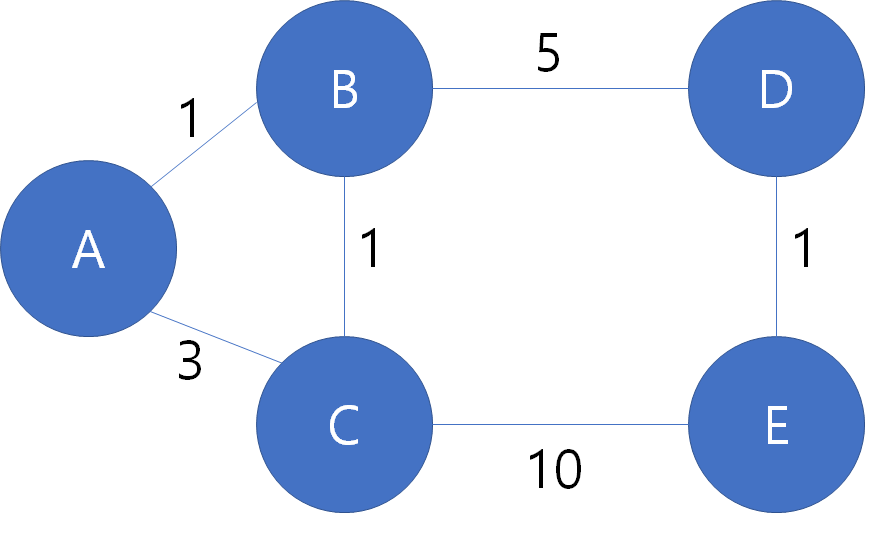
1. 모든 노드의 최소 거리 값 (dist)를 inf (무한대)로 잡는다. 시작 노드 (A)의 값은 0으로 한다.
| node | A | B | C | D | E |
| dist | 0 | inf | inf | inf | inf |
2. A노드와 연결된 B, C 노드에 대해 계산한다. B, C 노드 모두 현재 inf 값이므로
B: 1+0 < dist[B]=inf, C: 3+0 < dist[C]=inf 에 의해 각각 1, 3으로 갱신한다. 그리고 큐에 B, C를 넣는다. (우선순위 B가 더 높음)
| node | A | B | C | D | E |
| dist | 0 | 1 | 3 | inf | inf |
큐 : B(1), C(3) ( 노드(거리) )
3. 우선순위가 B가 더 높으므로 B와 연결된 노드에 대해 계산한다. B와 연결된 노드는 A, C, D이다.
A의 값은 0이므로 넘어간다. C의 값은 3이고 dist[B]+1 < 3 이므로 C는 2로 갱신된다.
D의 값은 inf 였으므로 D = min(inf, 5+dist[B]) = 6이다.
큐에 C, D를 넣는다.
| node | A | B | C | D | E |
| dist | 0 | 1 | 2 | 6 | inf |
큐 : C(2), C(3), D(6) => 같은 C이므로 C(2)만 생각하도록 하자. C(2)에 의해 갱신된 노드는 C(3)에 의해 갱신될 수 없다.
4. 큐의 top인 C(2)에 대해 계산한다. C와 연결된 노드는 A, B, E이고, A, B는 위와 마찬가지로 갱신되지 않는다.
( dist[A]=0 < 3+dist[C]=5, dist[B]=1 < 1+dist[C]=2 )
E만 dist[E]=inf > 10+dist[C]=12 이므로 갱신이된다. 큐에 E(12)를 넣는다.
C(3)에 대해서는 체크하지 않아도 된다.
D(6)와 연결된 노드가 B, E이다. B는 이미 체크가 완료되었으므로, E만 확인하자. dist[E]=12 > 1+dist[D]=7 이므로 E는 7로 갱신된다. 큐에 E(7)을 넣는다.
| node | A | B | C | D | E |
| dist | 0 | 1 | 2 | 6 | 7 |
큐 : E(7), E(12)
5. 큐에 E의 정보가 있지만, 나머지 노드에 대해 모두 체크를 완료하였으므로 A를 출발점으로 하는 가장 최단 거리는 B=1, C=2, D=6, E=7 임을 알 수 있다.
위와 같이 우선순위 큐를 이용하여 다익스트라 알고리즘을 적용할 수 있습니다.
코드는 다음과 같습니다.
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
int n, m;
vector<pair<int, int>>v[1001]; // [i] : 출발, {도착, 가중치}
int dist[1001];
int From, To;
void make_map()
{
cin >> n;
cin >> m;
for (int i = 0; i < m; i++) {
int from, to, weight;
cin >> from >> to >> weight;
v[from].push_back({ to,weight });
}
cin >> From >> To;
// 다익스트라 : 처음 모두 inf로 초기화
for (int i = 1; i <= n; i++)
dist[i] = 987654321;
}
// 우선순위 큐 이용한 다익스트라
void dijkstra(int start)
{
dist[start] = 0; // 시작점은 0으로 초기화
// 기본 오름차순, 가중치 작은 순으로 계산하므로
// 음의 가중치 넣어야 함
priority_queue<pair<int, int>>pq; // {가중치, 노드}
pq.push({ 0,start });
while (!pq.empty())
{
int d = (-1) * pq.top().first; // 가중치 양수로 변환
int current = pq.top().second;
pq.pop();
// 계산된 경로가 지금 꺼낸 경로보다 작으면 계산할 필요 없음
if (dist[current] < d)
continue;
// 가능한 경로 검사
for (int i = 0; i < v[current].size(); i++) {
int next = v[current][i].first;
int next_d = d + v[current][i].second;
// 경로 갱신
if (dist[next] > next_d) {
dist[next] = next_d;
pq.push({ (-1) * next_d, next });
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
make_map();
dijkstra(From);
cout << dist[To];
}'알고리즘 > 백준' 카테고리의 다른 글
| 백준 / 10422 괄호 C++ (1) | 2021.03.05 |
|---|---|
| 백준 / 2252 줄 세우기 C++ (0) | 2021.03.04 |
| 백준 / 1786 찾기 C++ (0) | 2021.03.01 |
| 백준 / 5014 스타트링크 C++ (0) | 2021.03.01 |
| 백준 / 1311 할 일 정하기 1 C++ (0) | 2021.02.24 |
