티스토리 뷰
2021 암호분석경진대회
CRYPTO ANALYSIS CONTEST
cryptocontest.kr

4번 문항은 부채널분석 문항입니다. 해당 암호화된 이미지와 전력분석 파일은 경진대회 홈페이지에 첨부되어 있습니다.
부채널분석 문항의 경우 작년에 상도 받았었기에 자신있었던 문항이었지만, 의외로 구해야 할 것이 너무 많아 실수할 부분이 많은 문제였습니다. 하지만 논문의 내용을 잘 따라가며 실수만 하지 않는다면 잘 풀 수 있습니다.

실제 암호화된 이미지의 경우 위와 같습니다. 이제 주어진 전력을 활용하여 이를 복구하고 키도 구해야합니다..... 제가 참고하였던 논문은 https://tches.iacr.org/index.php/TCHES/article/view/8392 입니다.
논문의 내용을 간단히 살펴보면 다음과 같습니다. AES128을 기준으로 논문이 작성되었습니다.
주제 : 부채널분석으로 AES-CTR 모드를 256개 trace만 이용해 깨보자!
AES에 이용된 블록의 상태는 다음과 같이 표시합니다.
1. 기본 형태

2. addround 형태

3. subbyte 형태

4. shiftrow 형태

5. mixcolumn 형태

6. 기타
CTR 모드에 사용된 Nonce 값을 N, Counter 값을 T 라 하며, 형태는 위와 같이 N0 ~ N15와 같이 16바이트 형태로 진행합니다.
해당 형태에 맞춰 간단히 논문을 설명하겠습니다.
1. 1바이트 공격하기
1-1 setup
256개의 trace를 활용하여 바이트 단위로 부채널 분석을 진행합니다. 그러므로 초기 Nonce 값의 carry 값이 15번째 바이트 (빅 엔디안 기준 맨 오른쪽 값, 0x FF EE DD ... 00 에서 00위치) 를 기준으로 14번째 바이트에 전달되는 carry는 무조건 0 아니면 1입니다.
그러므로 이 두 경우를 모두 고려하여 공격합니다.

1-2 1바이트 공격
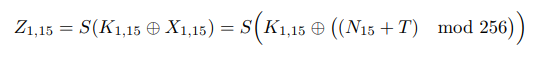
N15, T 값에 따라 sbox를 마친 결과 Z1,15를 다음과 같이 표시할 수 있습니다. 이를 간단히하면 다음과 같습니다.
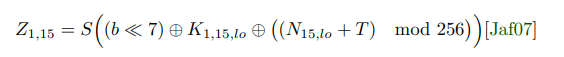
2. 4바이트 공격
1에서 Z1,15 위치 값을 부채널분석을 통해 알 수 있습니다. (Z1,14 위치까지 고려하여 후보군 2가지) 이제 mixcolumn 과정을 거친 X2,i 에 대해 다음과 같은 C 값을 부채널분석을 통해 구할 수 있습니다.
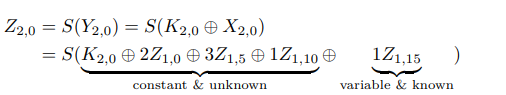
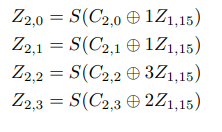
3. 16바이트 공격
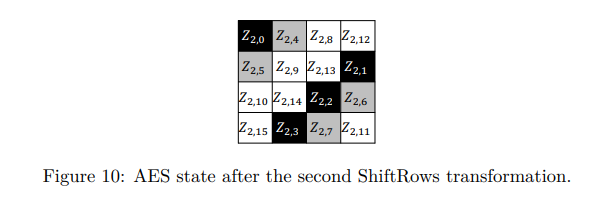
위 과정을 통해 처음 X1,15, X1,14 위치의 값을 이용해 색칠된 영역의 값을 추측할 수 있습니다. 이제 처음 고려하는 2가지 경우 X1,14에 전달되는 carry 0 또는 1 , 2가지 경우에 대해 X3,0 ~ X3,15 부분을 2번 공격과 마찬가지로 추측할 수 있습니다.
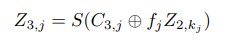
위에 나타낸 C 값만 잘 구하면 키를 복구할 수 있고, Nonce도 복구할 수 있습니다.
간략히 공격 포인트만 정리하였기 때문에 이해가 어려울 수 있지만, 논문을 찬찬히 읽으면 이해를 하실 수 있습니다.
이제 실제 ARIA128-CTR로 암호화된 이미지를 주어진 전력을 활용하여 복구해보겠습니다.
ARIA는 KISA에서 만든 AES 기반 블록암호입니다. ARIA도 동일한 블록암호이기에 해당 공격 방법이 적용 가능합니다. ARIA 알고리즘은 다음 링크에서 확인 가능합니다.
https://seed.kisa.or.kr/kisa/Board/19/detailView.do
KISA 암호이용활성화 - 자료실 - 암호알고리즘 소스코드
한국인터넷진흥원(KISA)에서는 128비트 블록암호 ARIA를 쉽게 활용할 수 있도록, 다양한 운영 모드에 대한 소스코드를 배포하고 있습니다. 언어 : C/C++, Java 운영 모드 : ECB, CBC, CTR, CFB, OFB, GCM, CCM, CMAC
seed.kisa.or.kr
1. 전력 및 ARIA 분석
주어진 전력을 분석하면 다음과 같습니다. 1~65535번째 블록에 대해 ARIA-CTR 연산을 진행하며, 마지막 블록은 원본 블록값을 가집니다.
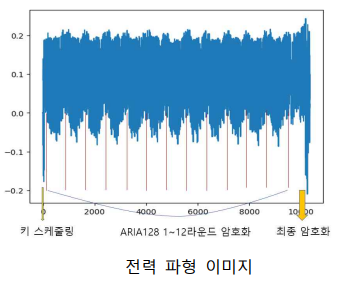
ARIA의 암호화는 간단히 다음과 같이 이루어집니다.
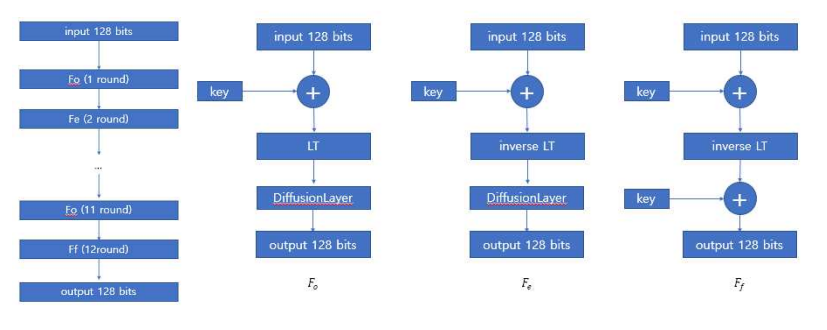
Fo 는 홀수 라운드, Fe는 짝수 라운드 Ff는 마지막 라운드입니다.
ARIA128에서 마스터키 MK를 이용하여 다음과 같은 W 값과 라운드 키 ek를 생성할 수 있습니다.
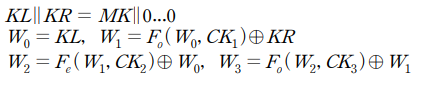

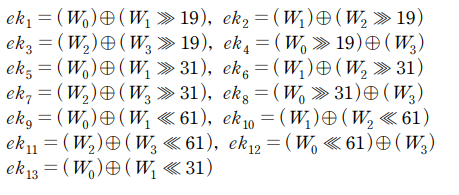
또한 블록암호에 사용되는 CTR 모드를 간단히 하면 다음과 같습니다.
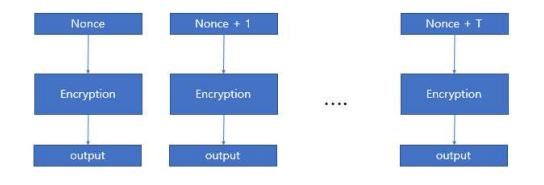
그리고 CPA 전력분석에 사용하는 Pearson 상관계수는 다음과 같습니다.

2. 키 복구
위 논문을 참고하여 키를 복구합니다. 256개의 trace만을 이용하므로 주어진 65536개 파형 중 처음 256개 파형만을 사용하였습니다. 0~255번째 trace 이용시 15번째 바이트 (0번째가 첫 번째) 에는 Nonce 값과 CTR 암호화에 이용된 T 값이 최대 255이므로 Nonce의 14번째 바이트에 전달되는 carry는 최대 1입니다.
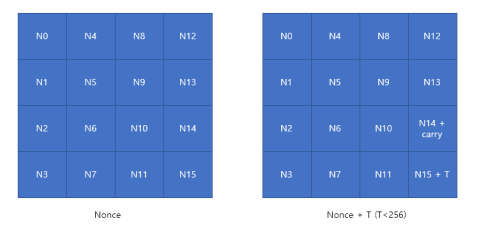
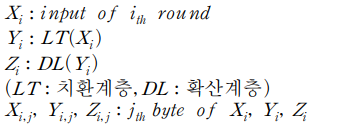
그리고 위처럼 정의 후 풀이를 진행하겠습니다.
초기 Z1,15의 15bit를 추측하기 위해 부채널분석을 진행합니다.
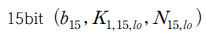
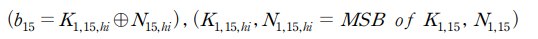
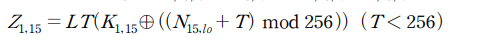
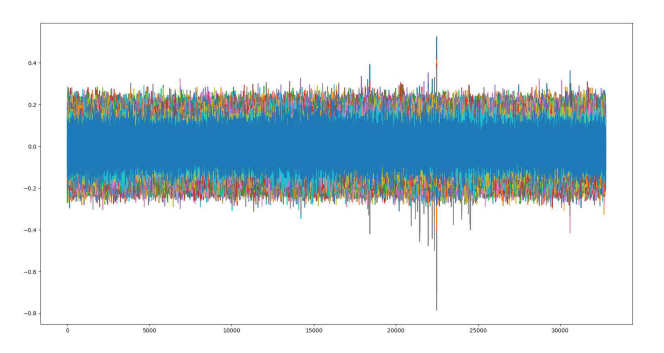
이 때 상관계수가 가장 높은 값은 22471 입니다. 이를 통해 다음과 같은 결과를 추측할 수 있습니다.
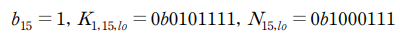
해당 결과를 이용하여 256개 trace에 해당하는 Z1,15를 구할 수 있고, ARIA의 확산계층에 대해 다음과 같이 적용할 수 있습니다.
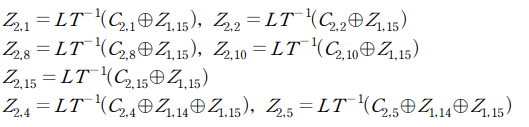
이제 carry에 영향을 받는 Z1,14 값을 Z1,15를 구하기 위한 과정과 동일하게 적용하기 위하여 0x0000, 0x0100, 0x0200, ..., 0xFF00 번째 전력을 활용하여 256개 블록만을 이용하여 15bit를 구합니다.
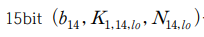
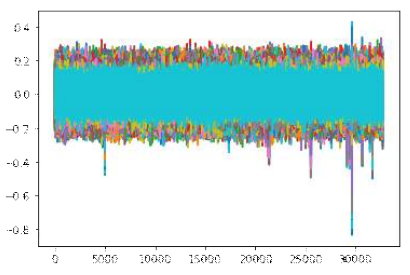
이를 통해 29646 일 때 가장 높은 상관계수를 얻을 수 있고, 다음과 같은 결과를 얻을 수 있습니다.
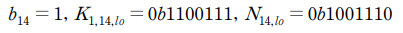
이를 이용하여 다음과 같은 case를 구분할 수 있습니다. (K1,14, N14, K1,15, N15 순)

위 논문에서 음영이 적용된 부분에 해당하는 C2,i 값을 케이스 별로 구할 수 있습니다.
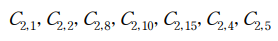
case1, 3 인 경우 C2,i 값은 다음과 같습니다.
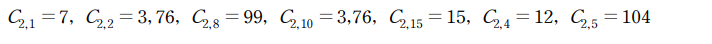
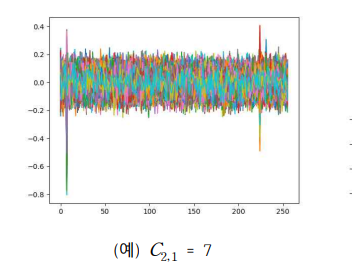
case2, 4 인 경우 C2,i 값은 다음과 같습니다.
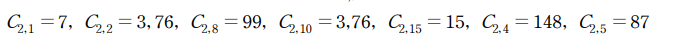
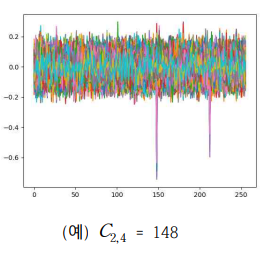
case1,2,3,4 모두에서 C2,2 C2,10의 값이 3 또는 76이 발생하므로 다음과 같은 4가지 경우가 모든 case에 적용할 수 있습니다.
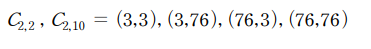
그러므로 총 16가지의 case에 대해 다음 식을 적용할 수 있습니다.
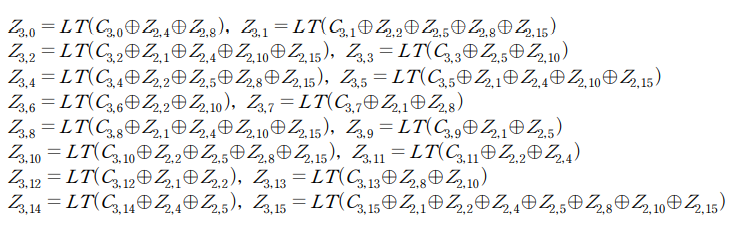
16가지 경우 중 부채널분석이 올바르게 이루어지는 경우는 case2,4 이며 C2,2 , C2,10 = 76, 3 일 때 발생하였습니다. 이 때 구할 수 있는 C3,i 값은 다음과 같습니다.
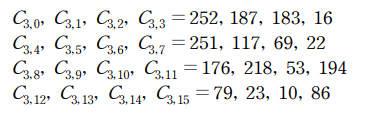
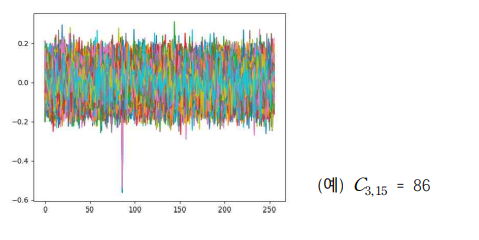
이제 C3,i 값을 알고 있으므로 Z3,i를 구할 수 있고, 4라운드 키를 부채널분석을 통해 복구할 수 있습니다. 구한 4라운드 키는 다음과 같습니다.

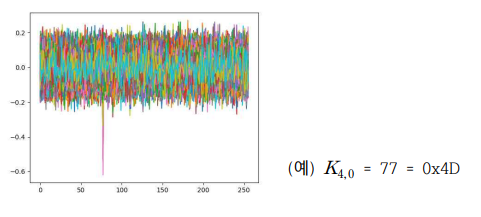
이제 키스케줄링을 통해 마스터키를 구하기 전에 ARIA128에서 5,6,7라운드 키를 구해야 합니다.
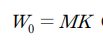
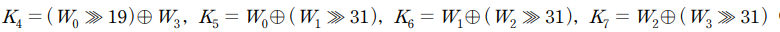
이와 같으므로 다음과 같습니다. 그러므로 5,6,7라운드 키가 필요합니다.
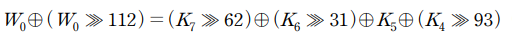
마찬가지로 부채널분석 결과 다음을 얻을 수 있습니다.

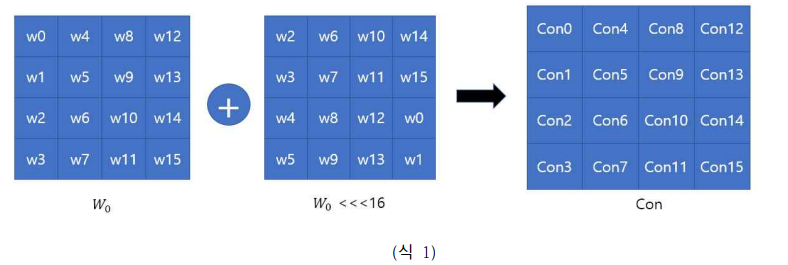
계산에 필요한 값을 Con으로 간략히 나타내겠습니다.
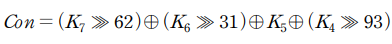
case2,4 에서 1라운드 키 K1의 일부를 알고 있으므로 P를 다음과 같이 잡습니다. (계산 편의 용 P)
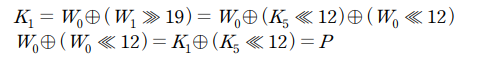
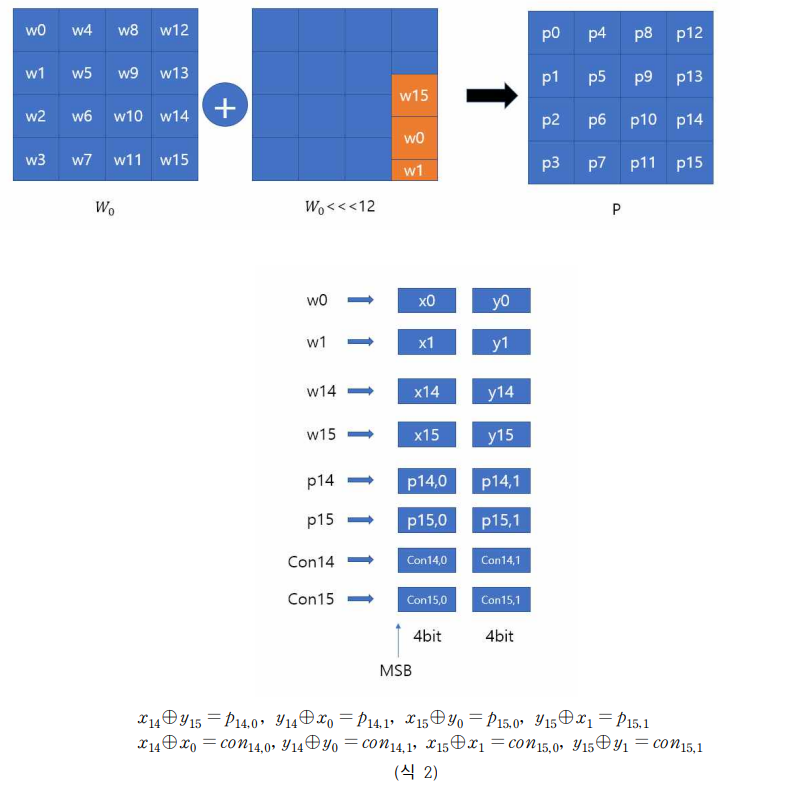
식1,2 를 이용해 다음을 유도할 수 있습니다.
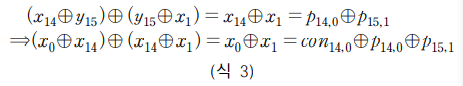
4bit x0 를 0~15까지 case2, 4 에 대입하여 K1과 비교하였을 때 올바른 결과를 가져오는 것을 계산하면 됩니다. 이 떄 K1 과 동일한 결과를 얻는 것은 case4, x0=6 일 때 입니다. 이를 통해 마스터키를 복구하면 다음과 같습니다.
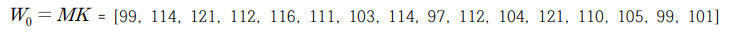
아스키코드로 변환시 cryptographynice 입니다 ㅎㅎㅎ
3. 초기 카운터 복구
초기 카운터의 경우 T=0 블록을 이용하면 쉽게 구할 수 있습니다. 3라운드까지 암호화된 결과를 알고 있기에 이를 역추적하면 됩니다.
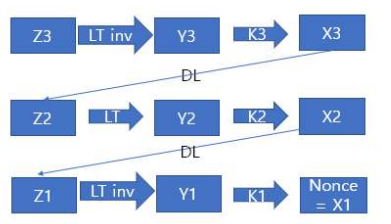
이를 통해 복구한 초기 카운터 값은 다음과 같습니다.
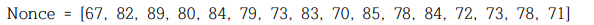
아스키코드로 변환시 CRYPTOISFUNTHING 입니다 ㅎㅎㅎ
4. 이미지 복구
카운터 값과 키를 알게 되었으므로 복호화를 진행합니다. 결과는 다음과 같습니다.

5. 코드 및 후기
단순히 AES128-CTR로 암호화된 것이 아닌 ARIA를 이용하여 암호화하였기 때문에 ARIA 알고리즘에 대한 이해가 필요한 문제였습니다. 더불어 256개의 trace만을 이용하여 부채널분석을 실시하는 새로운 공격방법도 알게 되었습니다. 처음에 논문을 이해하는데 조금 어려웠지만, 한 번 이해하고 나니 부채널분석을 계속 돌리는 시간 싸움이었습니다. (1주일 정도 컴터 계산만 시킨 듯....)
case가 여러 가지가 나왔기 때문에 각각을 모두 고려해야하여 햇갈렸습니다. 처음에 값을 잘못 메모했다가 3라운드 쯤에 결과가 나와야하는데 모든 case에서 아니라 하여서 어디서 잘못된 건지 찾기 위해 처음부터 다시 돌려봤던 기억이 있습니다. ㅠㅠ 역시 부채널분석은 쉽지 않습니다....
코드의 경우 각 라운드 별로 따로 파일을 만들어 부채널분석을 실시하였지만 결국 C2,i 값을 찾는 것과 동일하기 때문에 해당 코드만 올리겠습니다.
"""
현재 구한 것 Z1,15 (정확히는 b, K1,15,lo, N15,lo)
ARIA Diffusion Layer와 CPA 이용해서 Z2,1 Z2,4 Z2,10, Z2,15 구하기
Z1,15 = Sbox[(b<<7) ^ K1,15,lo ^ (N15,lo + T mod 256)]
b = 1
K1,15,lo = 0b0101111
N15,lo = 0b1000111
"""
%matplotlib qt5
import numpy as np
import matplotlib.pyplot as plt
import struct
Sbox = [
# S1
[
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16
],
# S2
[
0xe2, 0x4e, 0x54, 0xfc, 0x94, 0xc2, 0x4a, 0xcc, 0x62, 0x0d, 0x6a, 0x46, 0x3c, 0x4d, 0x8b, 0xd1,
0x5e, 0xfa, 0x64, 0xcb, 0xb4, 0x97, 0xbe, 0x2b, 0xbc, 0x77, 0x2e, 0x03, 0xd3, 0x19, 0x59, 0xc1,
0x1d, 0x06, 0x41, 0x6b, 0x55, 0xf0, 0x99, 0x69, 0xea, 0x9c, 0x18, 0xae, 0x63, 0xdf, 0xe7, 0xbb,
0x00, 0x73, 0x66, 0xfb, 0x96, 0x4c, 0x85, 0xe4, 0x3a, 0x09, 0x45, 0xaa, 0x0f, 0xee, 0x10, 0xeb,
0x2d, 0x7f, 0xf4, 0x29, 0xac, 0xcf, 0xad, 0x91, 0x8d, 0x78, 0xc8, 0x95, 0xf9, 0x2f, 0xce, 0xcd,
0x08, 0x7a, 0x88, 0x38, 0x5c, 0x83, 0x2a, 0x28, 0x47, 0xdb, 0xb8, 0xc7, 0x93, 0xa4, 0x12, 0x53,
0xff, 0x87, 0x0e, 0x31, 0x36, 0x21, 0x58, 0x48, 0x01, 0x8e, 0x37, 0x74, 0x32, 0xca, 0xe9, 0xb1,
0xb7, 0xab, 0x0c, 0xd7, 0xc4, 0x56, 0x42, 0x26, 0x07, 0x98, 0x60, 0xd9, 0xb6, 0xb9, 0x11, 0x40,
0xec, 0x20, 0x8c, 0xbd, 0xa0, 0xc9, 0x84, 0x04, 0x49, 0x23, 0xf1, 0x4f, 0x50, 0x1f, 0x13, 0xdc,
0xd8, 0xc0, 0x9e, 0x57, 0xe3, 0xc3, 0x7b, 0x65, 0x3b, 0x02, 0x8f, 0x3e, 0xe8, 0x25, 0x92, 0xe5,
0x15, 0xdd, 0xfd, 0x17, 0xa9, 0xbf, 0xd4, 0x9a, 0x7e, 0xc5, 0x39, 0x67, 0xfe, 0x76, 0x9d, 0x43,
0xa7, 0xe1, 0xd0, 0xf5, 0x68, 0xf2, 0x1b, 0x34, 0x70, 0x05, 0xa3, 0x8a, 0xd5, 0x79, 0x86, 0xa8,
0x30, 0xc6, 0x51, 0x4b, 0x1e, 0xa6, 0x27, 0xf6, 0x35, 0xd2, 0x6e, 0x24, 0x16, 0x82, 0x5f, 0xda,
0xe6, 0x75, 0xa2, 0xef, 0x2c, 0xb2, 0x1c, 0x9f, 0x5d, 0x6f, 0x80, 0x0a, 0x72, 0x44, 0x9b, 0x6c,
0x90, 0x0b, 0x5b, 0x33, 0x7d, 0x5a, 0x52, 0xf3, 0x61, 0xa1, 0xf7, 0xb0, 0xd6, 0x3f, 0x7c, 0x6d,
0xed, 0x14, 0xe0, 0xa5, 0x3d, 0x22, 0xb3, 0xf8, 0x89, 0xde, 0x71, 0x1a, 0xaf, 0xba, 0xb5, 0x81
],
# inverse S1
[
0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb,
0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb,
0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e,
0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25,
0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92,
0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84,
0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06,
0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b,
0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73,
0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e,
0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b,
0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4,
0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f,
0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef,
0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d
],
# inverse S2
[
0x30, 0x68, 0x99, 0x1b, 0x87, 0xb9, 0x21, 0x78, 0x50, 0x39, 0xdb, 0xe1, 0x72, 0x09, 0x62, 0x3c,
0x3e, 0x7e, 0x5e, 0x8e, 0xf1, 0xa0, 0xcc, 0xa3, 0x2a, 0x1d, 0xfb, 0xb6, 0xd6, 0x20, 0xc4, 0x8d,
0x81, 0x65, 0xf5, 0x89, 0xcb, 0x9d, 0x77, 0xc6, 0x57, 0x43, 0x56, 0x17, 0xd4, 0x40, 0x1a, 0x4d,
0xc0, 0x63, 0x6c, 0xe3, 0xb7, 0xc8, 0x64, 0x6a, 0x53, 0xaa, 0x38, 0x98, 0x0c, 0xf4, 0x9b, 0xed,
0x7f, 0x22, 0x76, 0xaf, 0xdd, 0x3a, 0x0b, 0x58, 0x67, 0x88, 0x06, 0xc3, 0x35, 0x0d, 0x01, 0x8b,
0x8c, 0xc2, 0xe6, 0x5f, 0x02, 0x24, 0x75, 0x93, 0x66, 0x1e, 0xe5, 0xe2, 0x54, 0xd8, 0x10, 0xce,
0x7a, 0xe8, 0x08, 0x2c, 0x12, 0x97, 0x32, 0xab, 0xb4, 0x27, 0x0a, 0x23, 0xdf, 0xef, 0xca, 0xd9,
0xb8, 0xfa, 0xdc, 0x31, 0x6b, 0xd1, 0xad, 0x19, 0x49, 0xbd, 0x51, 0x96, 0xee, 0xe4, 0xa8, 0x41,
0xda, 0xff, 0xcd, 0x55, 0x86, 0x36, 0xbe, 0x61, 0x52, 0xf8, 0xbb, 0x0e, 0x82, 0x48, 0x69, 0x9a,
0xe0, 0x47, 0x9e, 0x5c, 0x04, 0x4b, 0x34, 0x15, 0x79, 0x26, 0xa7, 0xde, 0x29, 0xae, 0x92, 0xd7,
0x84, 0xe9, 0xd2, 0xba, 0x5d, 0xf3, 0xc5, 0xb0, 0xbf, 0xa4, 0x3b, 0x71, 0x44, 0x46, 0x2b, 0xfc,
0xeb, 0x6f, 0xd5, 0xf6, 0x14, 0xfe, 0x7c, 0x70, 0x5a, 0x7d, 0xfd, 0x2f, 0x18, 0x83, 0x16, 0xa5,
0x91, 0x1f, 0x05, 0x95, 0x74, 0xa9, 0xc1, 0x5b, 0x4a, 0x85, 0x6d, 0x13, 0x07, 0x4f, 0x4e, 0x45,
0xb2, 0x0f, 0xc9, 0x1c, 0xa6, 0xbc, 0xec, 0x73, 0x90, 0x7b, 0xcf, 0x59, 0x8f, 0xa1, 0xf9, 0x2d,
0xf2, 0xb1, 0x00, 0x94, 0x37, 0x9f, 0xd0, 0x2e, 0x9c, 0x6e, 0x28, 0x3f, 0x80, 0xf0, 0x3d, 0xd3,
0x25, 0x8a, 0xb5, 0xe7, 0x42, 0xb3, 0xc7, 0xea, 0xf7, 0x4c, 0x11, 0x33, 0x03, 0xa2, 0xac, 0x60
]
]
HW=[
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8
]
with open('./trace.bin', 'rb') as f:
data = f.read()
f.close()
wave_cnt = 65536
time_cnt = 10340
time_float = time_cnt * 4
trace = []
for i in range(0, time_float * 256, time_float):
subtrace = []
subdata = data[ i : i + time_float ] # 파형 하나
# 마지막에 8byte 버리기
if len(subdata) < time_float:
continue
# bytes to float, 800~1600번째 시점만 (2라운드 전력)
# unpack 리턴 = 튜플 : (float,)
for j in range(3200, 6400, 4):
float_data = struct.unpack('f', subdata[ j : j + 4 ])
subtrace.append(float_data[0])
trace.append(subtrace)
def correlation(NP_trace, Ham):
# NP_trace : 전력 (numpy) = W, Ham : hamming weight (numpy)
n = len(NP_trace)
Sum_Wi = sum(NP_trace) # sigma Wi
Sum_Wi2 = sum(NP_trace ** 2) # sigma Wi^2
Sum_WiH = 0 # sigma WiHi,R
Sum_H = sum(Ham) # sigma Hi,R
Sum_H2 = sum(Ham ** 2) #sigma Hi,R^2
WH = [0 for _ in range(n)]
for i in range(n):
WH[i] = NP_trace[i] * Ham[i]
Sum_WiH = sum(WH)
return ( (n * Sum_WiH) - (Sum_Wi * Sum_H) ) / ( (((n * Sum_Wi2) - (Sum_Wi ** 2)) ** 0.5) * (((n * Sum_H2) - (Sum_H ** 2)) ** 0.5) )
# case = (K1,14, N14, K1,15, N15)
case1 = (0b01100111, 0b11001110, 0b00101111, 0b11000111)
case2 = (0b01100111, 0b11001110, 0b10101111, 0b01000111)
case3 = (0b11100111, 0b01001110, 0b00101111, 0b11000111)
case4 = (0b11100111, 0b01001110, 0b10101111, 0b01000111)
corr = [ [0 for _ in range(len(trace[0]))] for __ in range(2**8) ]
NP_trace = np.array(trace)
# num = C2,1 위치
# case 2가지 : N15,hi = 0 or 1
#b = 1
#K = 0b0101111
#N = N_case1
K1_14, N14, K1_15, N15 = case4
Ham = [0 for _ in range(len(trace))]
for num in range(2**8):
for t in range(len(trace)):
#Y = (b << 7) ^ K ^ ((N + t) % 256)
#Z1_15 = Sbox[3][Y] # Z1_15 = Z1,15
#Z2_10 = Sbox[0][num ^ Z1_15] # Z2_i = Z2,i
#Ham[t] = HW[Z2_10]
X1_15 = (N15 + t) % 256
carry = 0
if (N15 + t) >= 256:
carry = 1
X1_14 = (N14 + carry)
Y1_15 = X1_15 ^ K1_15
Y1_14 = X1_14 ^ K1_14
Z1_15 = Sbox[3][Y1_15]
Z1_14 = Sbox[2][Y1_14]
#Z2_4 = Sbox[2][num ^ Z1_14 ^ Z1_15]
Z2_5 = Sbox[3][num ^ Z1_14 ^ Z1_15]
Ham[t] = HW[Z2_5]
Ham = np.array(Ham)
for times in range(len(trace[0])):
corr[num][times] = correlation(NP_trace[ : , times], Ham)
if num % 50 == 0:
print(num)
# C2,i 값 구하기
plt.plot(corr)
'암호학 > 2021 암호경진대회' 카테고리의 다른 글
| 2021 암호분석경진대회 6번 풀이 (0) | 2021.11.23 |
|---|---|
| 2021 암호분석경진대회 3번 풀이 (0) | 2021.11.22 |
| 2021 암호분석경진대회 소감 (6) | 2021.11.22 |
