티스토리 뷰
고려대 정보보호대학원 2022학년 전기 석사 신입생으로 입학하게 되었습니다. 컨택한 연구실 랩장 형님께서 공부해오라고 하신 blind signature 내용을 간단히 정리하겠습니다.
https://sceweb.sce.uhcl.edu/yang/teaching/csci5234WebSecurityFall2011/Chaum-blind-signatures.PDF
David Chaum이 1983년 발표한 blind signature는 서명하는 사람이 서명하는 내용이 어떤 것인지 모르게하기 위한 것입니다.
논문 원본 내용을 그대로 빌려 쓰자면,
"어음과 같은 익명 지불 시스템은 통제와 보안에 취약하다. 지불에 대한 증명 부족과 훔쳐진 것인지, 암시장에 의한 것인지 등의 문제가 있다." 로 표현합니다.
(지금은 은행 시스템이 잘 되어 있지만 초기에는 그러지 못했나 봅니다. IMF 발생 전 한국에서도 어음을 마구 발행했다가 휴지조각이 된 것처럼 Chaum 형님도 당시 익명 전자 거래 시스템에 대해 불신했나 봅니다.... (제 생각))
- Basic Idea -
Blind signature의 기본 아이디어는 다음과 같습니다.
투표 시 투표자는 투표 내용을 알리고 싶지 않다. (누가 누구에게 투표한 것인지, 관리자 (서명자) 가 내가 누구에게 투표했는지를 모르게 하고 싶다.) 이러한 비밀을 유지하면서 내 투표 내용이 반영되길 원한다면 어떻게 해야 할까.
=> 특별한 용지와 봉투를 쓰면 된다!
(논문에서의 carbon paper = 먹지, carbon lined envelope = 먹지 봉투 라 해석했습니다. 먹지의 특성은 그 아래에 종이를 깔고 먹지에 뭔가를 적으면 종이에도 같은 내용이 적히는 것입니다. 이러한 특성을 비유하여 blind signature를 설명하고 있습니다.)
1. 투표자 (elector)는 먹지 (paper 1) 에 투표 내용을 적고 먹지 봉투 (envelope A) 에 paper 1 을 넣습니다. 그리고 그냥 봉투 (envelope B)에 자신의 반송 주소 (return address) 와 수신인 (관리자 = 서명자 = trustee) 를 적어 trustee에게 보냅니다.

2. trustee 는 envelope B 를 받았고 뜯어 envelope A를 확인합니다. 그리고 envelope A 위에 서명 (signature)을 합니다. 그리고 서명된 envelope A 를 그냥 봉투 envelope C 에 넣어 return address 로 다시 보냅니다.
=> 이 상황에서 trustee 는 투표 내용 m 이 어떤 내용인지 모른 채 서명을 진행하게 되고, envelope A 를 뜯어 확인한다면 그것은 elector 가 envelope A가 뜯겨진 것을 보고 trustee 를 못 믿게 되므로 소송이든 큰 일이 일어날지도 모릅니다. 결국 trustee 는 무슨 내용인지 모르지만 자신의 서명을 진행하게 됩니다.

3. elector는 envelope C를 받고 뜯은 뒤 signature를 확인합니다. 그리고 envelope A는 먹지 봉투였으니 내부의 paper 1에도 signature 가 복사됨 또한 확인할 수 있습니다. 서명이 복사된 paper 1을 봉투 envelope D 에 넣어 수신인만 trustee로 적어 보냅니다.

4. trustee는 envelope D를 받고 뜯은 뒤 자신의 서명을 확인하고 투표 내용을 보고 카운트합니다.
이로써 elector는 자신이 누구인지 밝히지 않으면서 trustee가 서명한 투표를 투표 집계에 포함시킬 수 있게 됩니다.

※ 투표자의 내용이 반영이 됐는지 유무는?
투표 내용을 보고 trustee 가 반영을 안 시킬 수도 있고, 실수로 누락될 수도 있습니다. 이를 방지하기 위해 trustee는 모든 집계된 투표 용지를 공개하고, elector는 paper 의 먹지 특성 (섬유 패턴, 또는 자신만의 흔적 등 구분 가능한 특징) 을 이용하여 자신의 투표가 반영되었는지 확인할 수 있습니다. (현재의 hash와 같은 기능)
이렇게 확인하여도 elector가 아무 말도 trustee에게 하지 않으면 trustee는 누가 누구에게 투표한 것인지를 모르므로 기존 목표인 "누가 누구에게 투표한지 모르게 하자" 를 달성하였습니다.
- Functions -
Blind signature를 이용하기 위한 함수들은 다음과 같습니다.
1. signing function s' (only known for signer), inverse of s' : s (public known)
=> i.e. s(s'(x)) = x
=> 그리고 s 로 s' 유추 못해야 합니다. (s 는 서명자의 공개키, s' 은 개인키)
2. commuting function : c, inverse of c : c' (c, c' : only known for provider)
=> 수학에서 commutative 라 하면 a * b = b * a 성질을 만족하는 건데 함수에 적용한 걸 의미한 듯 합니다
(g * h = h * g)
=> c'( s'( c(x) ) ) = s'(x) 를 만족해야 합니다.
=> c(x)와 s' 으로 x를 유추 못해야 합니다. (위 투표 예시에서 원본 메시지를 숨기는 것을 의미)
3. redundancy checking : r
=> 서명의 중복을 방지하기 위한 함수 r 입니다. (해시 같은 기능)
- Protocols -
위 먹지 봉투를 이용한 투표 예시와 같이 프로토콜을 구성하면 다음과 같습니다.
1. Provider : r(x) 와 같이 random한 x를 고른다.
=> c(x) 를 만든다. => c(x) 를 signer에게 준다.
2. Signer : c(x)를 s' 으로 sign 한다.
=> s'(c(x))를 provider에게 준다. (즉, 원본 x 는 모른 채 서명을 진행)
3. Provider가 s'(c(x)) 를 c' 으로 벗긴다. (stripped)
=> c'( s'( c(x) ) ) = s'(x) 를 얻는다. (원본 x 에도 동일한 서명 복사)
4. public 한 s 를 이용해 s' 을 검증할 수 있다.
=> s(s'(x)) = x
=> 올바른 서명임을 확인할 수 있으며 r( s( s'(x) ) ) 로 서명 중복성을 확인할 수 있다.
- Properties -
blind signature에는 아래와 같은 보안 속성이 필요합니다.
1. digital signature : 누구나 s'(x) 를 확인할 수 있어야 한다.
(signer의 private key를 모르지만 적용한 서명 결과는 누구나 알 수 있어야 한다.)
2. blind signature : signer는 { s'(x) } 와 { s'( c(x) ) } 의 관계를 몰라야 한다.
(stripped 된 것과 unstripped 된 것의 상관관계를 몰라야 한다. 즉 원본 메시지의 서명과 봉투 서명의 관계를 몰라야 함)
3. conservation of signature : provider는 signer가 sign한 것에 대해 최대 1개의 stripped signature만 만들 수 있다.
(즉 s'(x) 가 중복되어서는 안 된다.)
(ther is no i, j s.t. s'(x_i) = s'(x_j) for all i, j)
- Untraceable Payments System -
blind signauture를 활용하여 은행 송금을 진행하는 프로세스입니다. 송금자 (payer) 는 은행 (bank) 에게 누구에게 보내는지에 대한 정보를 알리고 싶지 않습니다. 수신자 (payee) 는 추후 payer에게 받은 정보로 은행에 payer가 맡긴 돈을 받습니다. 송수신에 사용되는 돈은 모두 1$ 로 가정합니다.
(약간의 어음 같은 개념이지만 익명 디지털 송금에 맞춘 어음 개념이라고 생각하면 됩니다.)
bank : 어음에 서명을 하는 주체
payer : 어음을 만들고 서명을 푸는 주체
payee : 어음을 받는 주체
단계는 다음과 같습니다.
1) payer : r(x)와 같은 랜덤한 x를 고르고 , c(x)를 만든다.
2) c(x)를 bank에게 보낸다.
3) c(x) 에 서명을 하여 s'( c(x) ) 를 만들고 payer로부터 돈을 인출한다.
4) s'( c(x) ) 를 payer에게 준다.
5) payer는 s'( c(x) ) 를 벗긴다. c'( s' ( c(x) ) ) = s'(x) 를 이용해 원본 메시지 x에 서명이 됨을 확인한다.
6) s( s'(x) ) = x 임을 확인하여 올바른 서명인지 확인한다.
7) 지불을 위해 payee에게 s'(x) 를 준다.
8) payee 는 r( s( s'(x) ) ) 를 확인한다. (서명 중복 방지)
9) payee 는 bank에게 s'(x) 를 준다.
10) bank 는 r( s( s'(x) ) ) 를 확인한다.
11) 기존 서명과 중복되는 지 확인 후 어음 리스트에 해당 내용 추가한다.
12) payee 에게 해당 금액을 입금한다.
13) 완료
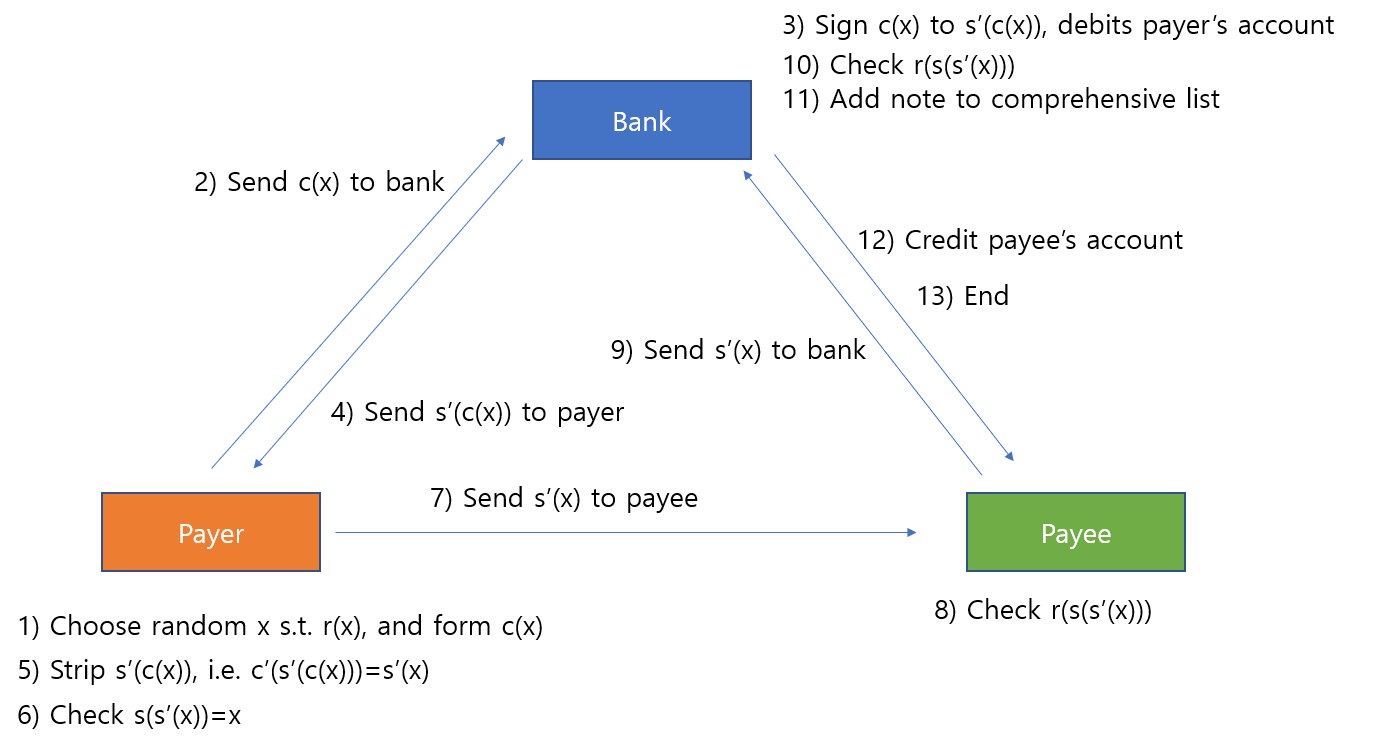
이 과정을 통해 bank는 payee에게 자신이 한 서명을 확인하였으므로 돈을 줘야하지만, 누가 payee에게 주는 지는 모릅니다.
예를 들어 payer1이 메시지로 "payee1에게 1달러 줘야 함. 아니면 고소할 거야." 라고 적었다고 가정하고, payer2는 메시지로 "payee1에게 1달러 줘야 함. 안 줘도 상관없고." 라고 적었다고 합시다. bank는 서명 과정에서 원본 메시지는 모르는 상황으로 payer1, payer2로부터 예치금을 각 1$ 씩 받은 상황이며, 숨겨진 메시지에 서명을 진행하였습니다.
이후 payee1이 payer1, payer2로부터 원본 메시지에 서명된 bank의 서명을 받았고 이를 bank에 다시 보내면 bank는 자신의 서명이 맞으므로 payee1에게 1$를 2번 송금해야 합니다. 하지만 payer1, payer2 중 누가 협박 메시지를 보냈는지는 bank는 알 수 없습니다.
이처럼 서명 진행 전 기존 메시지의 내용을 숨기고자 진행하는 방법이 blind signature이고, 위 과정을 바탕으로 추적 불가능한 송금 시스템이 완성됩니다.
- Blind RSA signature -
blind signature를 실제로 적용하기 위해 가장 간단한 blind rsa signature에 대해 정리하겠습니다.
blind rsa signature는 기존 rsa signature에 blind signature 개념을 얹은 것입니다.
기존 rsa 서명은 signer의 private key : d, public key : e, n (de = 1 mod phi(n)) 이라 하였을 때
메시지에 해시가 안 되었다는 가정하에 아래와 같습니다.
signauture :
verifying : check
이것을 이용해 blind rsa signature를 적용하면 다음과 같습니다.
1)
2) signer가
=>
(signer는 m에 대해 아무것도 알지 못한다.)
3)
4) sender는 다음을 확인할 수 있다.
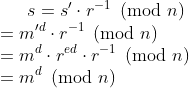
=> 이 결과로 sender는 원본 메시지 m 에 서명된 s 를 얻을 수 있다.
=> 즉, signer는 원본 메시지를 모른 채로 서명을 진행하게 된다.
- Danger of blind rsa signature -
blind rsa signature 는 하지 말아야 하는 규칙이 하나 있습니다. 바로 메시지를 암호화해서 서명을 받을 시 암호화를 아무렇게나 하면 안됩니다.
sender가 signer에게 서명을 받기 전 보통 해시 등으로 메시지를 압축하거나 암호화를 진행하게 되는데 이 때 signer의 공개키 e 로 m^e 로 암호화하여 서명을 받으면 attacker가 쉽게 원본 메시지를 얻을 수 있습니다.
1) sender :
2) sender가
3) attacker가 r을 알고 있다고 가정
4) signer가
5) attacker가
즉, blind rsa signature를 사용하려면 signer의 공개키로 암호화를 하여서는 안 됩니다.
######## 논문은 짧아 하루만에 읽었지만 정리하는데 좀 걸리네요... 역시 정리는 어렵습니다 ㅠㅜㅠㅜ
'암호학 > 이론' 카테고리의 다른 글
| Crystals-Dilithium 리뷰 (0) | 2022.12.11 |
|---|---|
| 동형암호 (2) | 2021.01.09 |
| SHA (0) | 2020.12.26 |
| Message Integrity and Message Authentication (0) | 2020.12.26 |
| Elgamal, ECC (0) | 2020.12.26 |
