티스토리 뷰
다익스트라 알고리즘은 그래프의 한 점에서 모든 점까지의 최단 경로를 구하는 알고리즘입니다.
(반드시 최단 경로만은 아니고 특정 조건에 해당하면 최소 거리 구하는 것 대신 해당 조건을 넣으면 됩니다.)
다익스트라 알고리즘 동작 과정은 다음과 같습니다.
1. 그래프가 주어지고, 시작점과 직접적인 연결이 없는 노드의 경우, 거리를 infinite 으로 지정한다. (아직 모른다고 침)
2. 시작점에서 가장 가까운 노드를 고른다.
3. 시작점에서 해당 노드와의 거리 (dist[x]) 와 해당 노드와 연결된 각 노드 간의 거리 (arr[x][y]) 가 기존 시작점에서 y 노드까지 거리보다 작으면 업데이트하고 해당 노드로 방문한다. (dist[x] + arr[x][y] < dist[y] => 업데이트)
4. 방문하지 않은 노드에 대해서 2,3 번을 반복한다.
총 N개의 노드가 있을 때, 가장 가까운 노드 고르기 => N번 수행, 고른 노드에서 다음 노드 고르기 => N번 수행이므로 총 복잡도는 O(N^2) 입니다.
기본 다익스트라 알고리즘에 대한 예시 그래프와 코드는 다음과 같습니다.

#include <iostream>
using namespace std;
#define INF 987654321
int get_nearest_node(int dist[], bool visited[], int nodeNum)
{
int minDist = INF;
int res = -1;
for(int i = 0; i < nodeNum; i++) {
// 이미 방문했던 경우 : 이미 해당 노드와 연결된 노드까지 거리는 업데이트함
if(visited[i])
continue;
if(dist[i] < minDist) {
minDist = dist[i];
res = i;
}
}
return res;
}
void dijkstra_basic(int startNode, int graph[5][5], int dist[], bool visited[], int nodeNum)
{
// 처음 dist 구하기
for(int i = 0; i < nodeNum; i++) {
dist[i] = graph[startNode][i];
visited[i] = false;
}
visited[startNode] = true;
for(int i = 0; i < nodeNum; i++) {
int nearestNode = get_nearest_node(dist, visited, nodeNum);
// 더 이상 업데이트할 게 없음
if(nearestNode == -1)
break;
visited[nearestNode] = true;
for(int j = 0; j < nodeNum; j++) {
dist[j] = min(dist[j], dist[nearestNode] + graph[nearestNode][j]);
}
}
}
int main()
{
int nodeNum = 5;
int graph[5][5] = {
{0, 3, 5, INF, INF},
{3, 0, 10, 7, 2},
{5, 10, 0, INF, 6},
{INF, 7, INF, 0, 3},
{INF, 2, 6, 3, 0},
};
for(int startNode = 0; startNode < nodeNum; startNode++) {
int *dist = new int[nodeNum];
bool *visited = new bool[nodeNum];
dijkstra_basic(startNode, graph, dist, visited, nodeNum);
// startNode 기준 각 노드까지 최단 거리
cout << "startNode " << startNode << " : ";
for(int node = 0; node < nodeNum; node++) {
cout << dist[node] << " ";
}
cout << "\n";
delete[] dist;
delete[] visited;
}
}

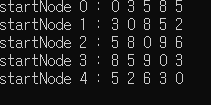
위와 같이 잘 계산됩니다.
기본 다익스트라 알고리즘을 좀 더 빠르게 동작시키기 위해 최소 힙 구조를 갖는 우선순위 큐를 사용할 수 있습니다.
우선순위 큐의 힙 구조에 의해 O(log N) 으로 가장 가까운 노드를 구할 수 있으므로 전체 복잡도는 O(N log N) 입니다.
코드는 다음과 같습니다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
#define INF 987654321
void dijkstra_pq(int startNode, int graph[5][5], int dist[], int nodeNum)
{
// 처음 dist 구하기
for(int i = 0; i < nodeNum; i++) {
dist[i] = INF;
}
dist[startNode] = 0;
// 우선순위 큐 기본적으로 내림차순
// greater 로 오름차순으로 변경
// pq <- {d, node} (d : 시작점에서 node까지 거리)
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>> > pq;
pq.push({0, startNode});
while(!pq.empty()) {
int d = pq.top().first;
int node = pq.top().second;
pq.pop();
// 업데이트 안 되는 경우
if(dist[node] < d)
continue;
// d, node 에는 탐색된 노드 중 가장 가까운 노드 저장 중
// 해당 노드를 기준으로 거리 업데이트
for(int nextNode = 0; nextNode < nodeNum; nextNode++) {
// 현재 탐색 노드 제외
if(node == nextNode)
continue;
if(dist[nextNode] > (d + graph[node][nextNode])) {
dist[nextNode] = d + graph[node][nextNode];
pq.push({dist[nextNode], nextNode});
}
}
}
}
int main()
{
int nodeNum = 5;
int graph[5][5] = {
{0, 3, 5, INF, INF},
{3, 0, 10, 7, 2},
{5, 10, 0, INF, 6},
{INF, 7, INF, 0, 3},
{INF, 2, 6, 3, 0},
};
for(int startNode = 0; startNode < nodeNum; startNode++) {
int *dist = new int[nodeNum];
dijkstra_pq(startNode, graph, dist, nodeNum);
// startNode 기준 각 노드까지 최단 거리
cout << "startNode " << startNode << " : ";
for(int node = 0; node < nodeNum; node++) {
cout << dist[node] << " ";
}
cout << "\n";
delete[] dist;
}
}
'알고리즘' 카테고리의 다른 글
| 벨만 포드 정리 C++ (2) | 2024.04.21 |
|---|---|
| 플로이드 워셜 C++ (0) | 2024.04.21 |
| 위상정렬 정리 C++ (위상정렬 모든 탐색 결과 포함) (0) | 2024.04.21 |
| binary search 구현 C++ (중복 가능, 값 없는 경우 포함) (1) | 2024.04.20 |
| permutation, combination 구현 C++ (0) | 2024.03.09 |
