티스토리 뷰
C++에서 map, set은 기본적으로 red black tree를 기준으로 만들어져 있다.
red black tree는 balanced binary tree로 특정 기준에 따라 좌우 tree가 균형있게 만들어진다.
(즉, 좌 작은 값, 우 큰 값일 때 큰 것만 계속 insert 되어 오른쪽 tree만 커지게 되는 문제 해결 등)
red black tree를 직접 구현하는 것은 다음 번에 정리한다.
(PS 같은 거에서 직접 tree 만들기는 너무 빡세므로 다음 번에....)
그렇다면 insert, erase, find 모두 O(log N) 으로 동작하므로 이에 대한 내용을 간단히 정리한다.
C++ 기본 타입 (int, double, string 등) 이 아닌 struct에 대해 map, set의 key로 설정하려면 다음과 같이 operator를 설정해야 한다.
struct Data {
pair<int, int> range;
int id;
};
struct Compare {
bool operator() (const Data &d1, const Data &d2) {
// tree 구성 시 아래 조건 따름
// 우선순위 (오름차순) : range.first, range.second, id
if(d1.range.first != d2.range.first)
return d1.range.first < d2.range.first;
if(d1.range.second != d2.range.second)
return d1.range.second < d2.range.second;
return d1.id < d2.id;
}
};
set<Data, Compare> s;
map<Data, int, Compare> m;
그리고는 기존과 동일하게 insert, find, erase 를 진행하면 된다.
erase 시에는 없는 key 값을 erase 하여도 별도 에러가 발생하지 않는다.
insert 대신 emplace 사용 시 pair<iter, bool> 타입이 리턴되고, first는 삽입된 iterator, second는 성공 여부 (중복 없었으면 true, 있었으면 false) 를 의미한다.
또한 map, set의 기본 operator는 less 이므로 단순 auto it = s.begin() 등으로 loop를 돌릴 시, 오름차순으로 출력된다.
(begin은 red black tree의 제일 마지막 depth 왼쪽 노드를 의미)
#include <iostream>
#include <map>
#include <set>
using namespace std;
struct Data {
pair<int, int> range;
int id;
};
struct Compare {
bool operator() (const Data &d1, const Data &d2) {
// tree 구성 시 아래 조건 따름
// 우선순위 (오름차순) : range.first, range.second, id
if(d1.range.first != d2.range.first)
return d1.range.first < d2.range.first;
if(d1.range.second != d2.range.second)
return d1.range.second < d2.range.second;
return d1.id < d2.id;
}
};
int main()
{
Data d[10];
d[0] = {{4,9},1};
d[1] = {{1,10},2};
d[2] = {{1,100},3};
d[3] = {{100,200},4};
d[4] = {{10,25},5};
d[5] = {{6,7},6};
d[6] = {{11,13},7};
d[7] = {{16,20},8};
d[8] = {{2,5},9};
d[9] = {{6,9},10};
set<Data, Compare> s;
map<Data, int, Compare> m;
for(int i = 0; i < 10; i++) {
s.insert(d[i]);
m.insert({d[i], i}); // == m[d[i]] = i
}
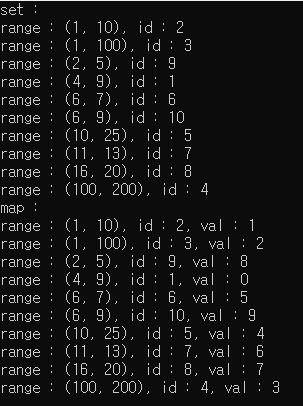
printf("set : \n");
for(auto it = s.begin(); it != s.end(); it++) {
printf("range : (%d, %d), id : %d\n", (*it).range.first, (*it).range.second, (*it).id);
}
printf("map : \n");
for(auto it = m.begin(); it != m.end(); it++) {
printf("range : (%d, %d), id : %d, val : %d\n", (it->first).range.first, (it->first).range.second, (it->first).id, it->second);
}
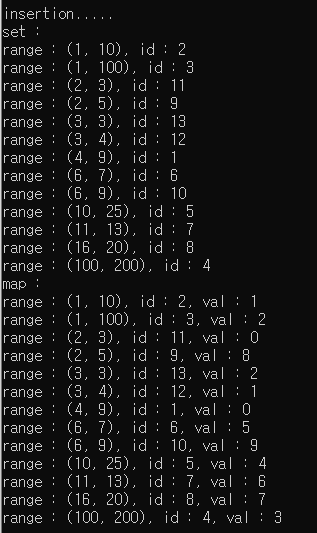
printf("\ninsertion.....\n");
Data d2[3];
d2[0] = {{2,3},11};
d2[1] = {{3,4},12};
d2[2] = {{3,3},13};
for(int i = 0; i < 3; i++) {
s.insert(d2[i]);
m.insert({d2[i], i});
}
printf("set : \n");
for(auto it = s.begin(); it != s.end(); it++) {
printf("range : (%d, %d), id : %d\n", (*it).range.first, (*it).range.second, (*it).id);
}
printf("map : \n");
for(auto it = m.begin(); it != m.end(); it++) {
printf("range : (%d, %d), id : %d, val : %d\n", (it->first).range.first, (it->first).range.second, (it->first).id, it->second);
}
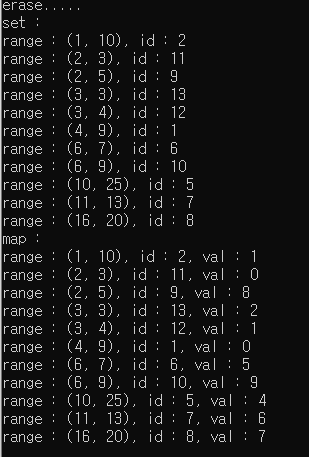
printf("\nerase.....\n");
Data d3[3];
d3[0] = {{1,100},3};
d3[1] = {{100,200},4};
d3[2] = {{-1,-1},-1};
for(int i = 0; i < 3; i++) {
s.erase(d3[i]);
m.erase(d3[i]);
}
printf("set : \n");
for(auto it = s.begin(); it != s.end(); it++) {
printf("range : (%d, %d), id : %d\n", (*it).range.first, (*it).range.second, (*it).id);
}
printf("map : \n");
for(auto it = m.begin(); it != m.end(); it++) {
printf("range : (%d, %d), id : %d, val : %d\n", (it->first).range.first, (it->first).range.second, (it->first).id, it->second);
}
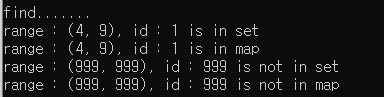
printf("\nfind.......\n");
Data d4[2];
d4[0] = {{4,9}, 1};
d4[1] = {{999,999},999};
for(int i= 0; i < 2; i++) {
if(s.find(d4[i]) != s.end()) {
printf("range : (%d, %d), id : %d is in set\n", d4[i].range.first, d4[i].range.second, d4[i].id);
}
else
printf("range : (%d, %d), id : %d is not in set\n", d4[i].range.first, d4[i].range.second, d4[i].id);
if(m.find(d4[i]) != m.end()) {
printf("range : (%d, %d), id : %d is in map\n", d4[i].range.first, d4[i].range.second, d4[i].id);
}
else
printf("range : (%d, %d), id : %d is not in map\n", d4[i].range.first, d4[i].range.second, d4[i].id);
}
}
결과
'알고리즘' 카테고리의 다른 글
| 36진법 덧셈, 절대값 뺄셈, 곱셈 (0) | 2024.10.04 |
|---|---|
| C++ lower_bound, upper_bound (0) | 2024.06.22 |
| Index Tree 로 구간 최대값, 최소값, 구간합 구하기 (0) | 2024.06.16 |
| combination, permutation 정리 (0) | 2024.05.01 |
| KMP 알고리즘 정리 (1) | 2024.05.01 |
